植物根系吸水模型研究进展

引用本文

王玉阳, 陈亚鹏.植物根系吸水模型研究进展. 草业学报, 2017,26(3): 214-225
WANG Yu-Yang, CHEN Ya-Peng.Research progress in water uptake models by plant roots. Acta Prataculturae Sinica,2017,26(3): 214-225 复制到剪切板

Permissions

《草业学报》编辑部

植物根系吸水模型研究进展

王玉阳^1,², 陈亚鹏^1*,^*

1.中国科学院新疆生态与地理研究所荒漠与绿洲生态国家重点实验室,新疆乌鲁木齐 830011

2.中国科学院大学,北京 100049

*通信作者Corresponding author. E-mail: chenyp@ms.xjb.ac.cn

作者简介:王玉阳(1991-),男,河南南阳人,在读硕士。E-mail: wangyuyang14@mails.ucas.ac.cn

收稿日期: 2016-04-05

基金项目:国家支撑计划课题(2014BAC15B02)和国家自然科学基金项目(41371515,41371503)资助

摘要

根系吸水是植物水分传输系统的最初端,直接控制着整株植物的水分传输量,进而影响植物的生命活动。对植物根系吸水的研究不仅是土壤-植物-大气连续体(SPAC)中水分运移规律研究的重要内容,同时也是水文、气候、土壤、农业、生态等多学科领域交叉研究的重点。根系吸水模型是定量化研究植物根系吸水的数学模拟工具。建立合适的根系吸水模型是准确估算植物根系吸水量的基础,这有助于弄清植物的需水特性和水分来源。本研究在总结根系吸水模型的基础上,概述了根系吸水的机理、不同研究尺度下的根系吸水模型的分类,并重点分析了实际应用较广泛的宏观根系吸水模型,且对每种模型应用的范围和局限性做出了说明。最后对现有根系吸水模型中存在的问题进行了初步分析,并对其未来研究方向和内容进行展望。

关键词: 根系; 吸水模型; 宏观; 研究进展

Research progress in water uptake models by plant roots

WANG Yu-Yang^1,², CHEN Ya-Peng^1,^*

1.State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China

2.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

The uptake of water by roots is the beginning of water transport within a plant, with such uptake directly controlling the amount of water available for transporting and, as a result, strongly affecting the life of the plant. Research on this uptake is thus not only a key to understanding the process of water transfer in the soil-plant-atmosphere continuum, but also an important topic for interdisciplinary research in such areas as hydrology, climate, soil, agriculture and ecology. Models for root uptake of water provide a numerical tool for quantitatively understanding this plant process. The establishment of a suitable model will provide not only a basic tool for estimating the amount of water absorbed but will also help to discover the water sources and requirements of plants. It can thus assist the development of effective agricultural water management programs, with far-reaching significance for restoring vegetation in extremely arid regions. In this paper, we review the development of models for root uptake of water, sum up the mechanisms identified and classify the models into different types at macroscopic and microscopic scales. We analyze the macroscopic models in detail, including Ohm’s law model, Feddes model, Transpiration segment model, Hybrid model, Compensatory root uptake water model and the Matric flux potential model, which are widely used in practical experiments. We illustrate the application range and discuss the limitations of existing models. We conclude with three suggestions for future research: 1) the establishment of dynamic models for root uptake of water, 2) the combination of microscopic and macroscopic models, and 3) the development of models for trees and herbages.

Keyword: root system; root water uptake models; macroscopic scale; recent advances

Show Figures

水对植物的生长必不可少, 植物需要通过根系不断的从土壤中吸收水分来满足叶片的蒸腾以维持植物有机体正常的生理活动^[1]。根对土壤水分的吸收和输送是土壤-植物-大气连续体系统(SPAC)的重要组成部分^[2], 定量研究土-根系统中水分的运动也是水文过程模拟中的主要环节^[3]。同时, 植物根系对水分的吸收不仅是地表水量平衡的主要部分, 而且也是控制地表、大气和植物生长之间能量交换的重要过程^[4]。根对土壤水分的吸收深刻影响着有植被覆盖的上层土壤水分含量的时空分布^[5], 植物根系和周围土壤之间水分传输的强度控制着植物地上部分的水分、气体和能量交换等生态生理过程^[6]。鉴于植物根系在地圈-生物圈-大气圈之间相互关联的纽带作用, 许多国际合作项目, 诸如国际生物圈地圈计划(IGBP)、世界气候研究计划(WCRP)等都将植物根系吸水作为其项目的核心研究主题, 根系吸水模型的构建也成为生态、水文、环境等科学领域研究的热点^[7]。

由于根吸收水分对植物生长的重要性, 根系吸水模型的构建一直是土壤学家、农学家和生态水文学家研究的焦点。但是, 根吸收水分的过程很复杂, 不仅受到基因控制、根的构型、根的密度分布、根对水分的阻力等内在因素的影响, 同时也受到土壤水分状况、土壤对水分传输的阻力、土壤营养水平、土壤温度、土壤通气状况、植物蒸腾等外在因素的影响^[8]。用数学模型来模拟根对土壤水分的吸收可以将问题简单化, 并且应用准确的模型可以使研究不需要实地测量就能得到可靠有效的数据^[9], 但是合适准确的根系吸水模型的构建是十分困难的, 因为根生长在地下难以观测, 进行剖面挖掘又会对根系造成破坏, 同时控制根吸水生理过程的知识还不够完善^[5], 所以根系吸水模型的研究还需进一步进行下去。

本研究综述了根系吸水模型的发展过程, 包括微观模型和宏观模型, 侧重于介绍实际应用较多的宏观根系吸水模型的发展, 并对相关模型中存在的局限性进行阐述并做出了一定的展望。

1 根系吸收水分的机理

根系吸收水分的机理十分复杂, 植物通过根系从土壤中吸收水分, 但根的不同部位对水分的吸收速率并不是一致的, 实际上根主要通过根尖的根毛区来吸收水分^[10]。根的发育时间, 新根和老根的更新速率, 根系在土壤区域中的空间分布, 以及土壤的理化性质、气象条件等的不同都会影响根系对水分的吸收^{[8, 11]}, 并导致根系吸水速率随空间和时间的变化而发生改变。

植物根系吸水主要有两种方式, 即主动吸水和被动吸水^[1]。主动吸水是在蒸腾作用弱的情况下由根内外水势差驱动的渗透流, 主动吸水需要植物消耗能量; 被动吸水是蒸腾作用下靠蒸腾拉力驱动的压力流来吸收水分, 植物主要通过被动吸水的方式来吸收水分。植物通过根系从土壤中吸收水分, 然后经过根木质部向上输送供给植物的新陈代谢活动, 根系从土壤中吸收水分包括两个途径, 径向途径和轴向途径。径向途径即水分由土壤跨过根组织(表皮、皮层、内皮层、中柱)到达根木质部, 包含了质外体运输、共质体运输和跨膜运输3个部分, 轴向途径是水分沿着根木质部向上输送的过程^[12]。

2 根系吸水模型

根据不同的划分标准, 根系吸水模型可以划分为不同的类型^[13], 依据研究尺度的不同, 将根系吸水模型主要划分为微观和宏观两个方面, 植物根系吸水模型的发展与分类见表1。

表1 根系吸水模型的分类和发展^[11~45] Table 1 Classification and development of root water uptake models^[11~45]

模型类型 Model types	子模型 Models					模型表达 Model expression	代表者及年份 Citations	模型优缺点 Advantages and disadvantages
微观模型 Micro-scopic models	单根尺度上径向流动的模型 Radial flow models build on a single root scale					Ψ _b-Ψ _a= $\begin{matrix} \frac{q}{4 πk} \end{matrix}$ ln $\begin{matrix} (\frac{b^{2}}{a^{2}}) \end{matrix}$	Gardner (1960)	建立的第一个根系吸水模型, 开创了该类模型研究的先河, 但是假设条件太多与实际不相符。The first root water uptake model, which serves as a precedent for the root water uptake model research. But, it is based on too many assumptions that are not generally meet in the actual conditions.
						q= $\begin{matrix} \frac{Ψ_{surf} - Ψ_{root}}{r_{root}} \end{matrix}$	Campbell (1985)	类似于电流输送的欧姆定律, 模型简单清晰, 但是阻力项难以界定。An Ohm’ m law model which is similar to current transfer. The model is simple, however, the resistance term is difficult to define.
宏观模型 Macro-scopic models	Ⅰ 型模型Type Ⅰ	基本模型The basic model	S=BKG	Nimah et al (1973), Cardon et al(1992)	模型构造简单清晰, 但是对盐分模拟不敏感。The composition of the model is simple, but it is insensitive to salinity simulation.
		欧姆定律模型 The Ohm’ s law model	S(z)= $\begin{matrix} \frac{σ (z)}{r_{soil} (z) + r_{root}} \end{matrix}$ [H_soil(z)-H_root]	Campbell (1985), Vogel et al (2013)	根土界面水势以及水分传输的阻力项难以界定。The matric potential at the soil-root interface and the resistance term of water transport are difficult to define.
	Ⅱ 型模型Type Ⅱ	Feddes模型 Feddes model	S_a(z)=α [h(z)]S_p(z)	Feddes et al (1978)	引入土壤水势响应函数, 考虑了不同深度土壤水势对根吸收水分的影响。忽略了根的分布对水分吸收的影响。The root water uptake reduction function was introduced, and considering the influence of soil water potential at each soil depth on root water uptake. However, it ignores the effect of the root spatial distribution.
		蒸腾分割模型 Transpiration segment model	S_p(z)=β (z)T_p	Feddes et al (1978)	根据根吸水的因果关系建立的模型, 理论清晰。但在分割蒸腾时仅考虑了根的分布因素, 不全面。The model is constructed based on the casual relationship of root water uptake. But it only considers the root factor when portioning the transpiration.
		耦合模型 The hybrid model	S_a(z)=β (z)α [h(z)]T_p	Hopmans et al (2002)	蒸腾分割模型与Feddes基本模型的耦合, 兼有这两种模型的优点, 但是没有考虑根在异质性的土壤水分剖面中的调节作用。The hybrid model of the basic model and portioning transpiration model. It has the advantages of both model, but it does not consider the root adjust function in the heterogeneous soil moisture.
		补偿机制模型 Compensatory root uptake water model	S_a(z)=T_pα [h(z)]β (z)φ S_a(z)=T_pα [h(z)]β (z)max $\begin{matrix} [1, \min (\frac{{α^{*}}_{\max}}{ω}, \frac{1}{ω_{c}})] \end{matrix}$	Jarvis(1989), Albasha et al (2015), Prters(2016)	综合考虑了多种因素的影响, 但是参数是经验性的, 机理性不充分。It takes into account many factors influencing the root water uptake processes, but the parameters are empirical.
		基质通量势模型Matric flux potential model	S=ρ (M-M₀)	Van lier et al (2006, 2008)	将微观机理引入到根吸水模型中, 使得该模型模拟的更加准确By incorporating the microscopic mechanism into the root water uptake model, it improves the simulation accuracy.
其他模型 Other models	水盐胁迫下的模型 Root water uptake model under water and salinity stress		S(h, h_φ, z)=α (h, h_φ, z)β (z, t)T_p(t)	Li et al (2015), Skaggs et al (2006)	在宏观Ⅱ 型模型中加入盐分胁迫项即可得到水盐共胁迫下的模型, 但是总的胁迫效应是两胁迫相加还是相乘仍不清楚。This model could simulate root water uptake under water and salinity stresses. However, the challenge is how to combine the effects of water and salinity stresses, additive or multiplicative?
	宏观微观相结合模型The combination of microscopic and macroscopic root water uptake model		$\begin{matrix} \frac{\partial θ}{\partial t} \end{matrix}$ =∇[k∇(h-z)]-S S_j= $\begin{matrix} \frac{\overset{ni}{\sum_{i}} J_{r, i}}{V_{j}} \end{matrix}$	Javaux et al (2008)	根吸水模型发展的趋势, 弥补了宏观微观模型各自模拟时的缺陷。It makes up for the drawbacks of the separate simulation by macroscopic and microscopic model.
	多维度根系吸水模型Multi-dimen-sional rootwater uptake model		S_m(x, y, z)= $\begin{matrix} \frac{β (x, y, z)}{\int_{0}^{x_{m}} \int_{0}^{y_{m}} \int_{0}^{z_{m}} β (x, y, z) dzdydx} \end{matrix}$ x_my_mT_p	Heinen et al (2014), Schroder et al (2009)	多维度根系吸水模型也是模型发展的趋势, 能够更准确的模拟实际情况, 难度很大。Multi-dimensional root water uptake model is the main direction of developing root water uptake model, which can accurately simulate the root water uptake processes, but it is difficult to build.

表1 根系吸水模型的分类和发展^[11~45] Table 1 Classification and development of root water uptake models^[11~45]

2.1 微观的根系吸水模型

微观的根系吸水模型是描述微观土壤区域内水分向根的运动, 是基于物理机制建立在单根尺度上的, 研究流向和进入典型单根的径向流, 侧重于描述根吸收水分的过程机理^[8]。微观模型是以Vandenhonert^[14]1948年提出的悬链线假说为基础的。在微观模型中, 土壤水分的流动被描述为柱面坐标中的运动^[3], 根附近区域土壤水分的运动方程可表示为:

$\begin{matrix} \frac{\partial θ}{\partial t} \end{matrix}$ = $\begin{matrix} \frac{1}{r} \end{matrix} \begin{matrix} \frac{\partial}{\partial r} \end{matrix} \begin{matrix} (rD \frac{\partial θ}{\partial r}) \end{matrix}$ (1)

式中:D是土壤水分的扩散率; t是时间; r是距离根木质部的径向距离; θ 是土壤含水率。

Gardner^{[11, 15]}在1960年建立了单根尺度上的根系吸水的数学模型, 原理就是用根表面以及距根木质部一定距离的合适的边界条件在方程(1)的基础上来建立根系吸水的微观模型。

Ψ _b-Ψ _a= $\begin{matrix} \frac{q}{4 πk} \end{matrix}$ ln $\begin{matrix} (\frac{b^{2}}{a^{2}}) \end{matrix}$ (2)

该模型基于一系列的假设, 认为根是无限延伸的圆柱体, 任意两相邻根之间的距离为2b, 根具有一致的半径a和吸水特性, 水分仅通过径向流入根内部, 根区起始的土壤水分状况相同。式中:Ψ _b是任意两相邻根中间部位土壤的水势; Ψ _a是根土界面的水势; q是单位根长单位时间内的吸水速率; k是非饱和土壤的导水率。

微观根吸水模型还有另外一种表示形式, 该模型假设水分在一定时期内在土壤-植物-大气连续体(soil-plant-atmosphere-continuum, SPAC)中的运动处于稳定状态, SPAC中的水势是连续的, 并由内聚力所控制。因此, 可以用模拟电流传输的欧姆定律来描述水分在这个连续体内的运动, 即SPAC系统中每个模块的水流通量由该模块的水势梯度和水分阻力所决定^[16]。这样就建立了基于水势梯度的欧姆定律模型:

q= $\begin{matrix} \frac{Ψ_{surf} - Ψ_{root}}{r_{root}} \end{matrix}$ (3)

式中:q是根吸收水分的速率; Ψ _surf是根土界面的水势; Ψ _root是根木质部的水势; r_root 是径向的根组织对水分传输的阻力。

微观尺度的根吸水模型从机理上阐释了根对土壤水分的吸收, 能够描述根区微域内土壤水分的运动规律。微观尺度的定量半定量研究能够对宏观尺度的根吸水模式存在的潜在误差进行校正和分析^[17]。但是此类模型建立的假设条件有许多都是与实际情形不相符的, 例如认为根是无限延伸的圆柱体、吸水特性沿根长不变、具有一致的半径等, 同时由于根系系统的结构很难获取, 并且随时间发生变化, 同时这种建立在单根尺度上的水分吸收模型很难扩展到整个根系系统^[8]。因而, 微观根系吸水模型在实际应用中就十分困难。但是微观的根系吸水模型开创了根系吸水模型研究的先河, 并为根系吸水模型的发展提供了理论依据和方法。

2.2 宏观的根系吸水模型

宏观的根系吸水模型将整个根-土系统看作一个整体, 忽略了根的水力特性。在实际应用中宏观模型比微观模型有着更多的优势, 宏观模型不需要弄清根吸水的全部过程机理, 这样就不必去研究那些难以界定的土壤和根的参数^[18]。同时宏观模型多是经验性的, 能够在田间或是野外直接应用。

宏观的根吸水模型的构建是在描述土壤水分运动的理查德方程上外加一个汇源项来实现的, 该汇源项表示根对水分的吸收速率。

$\begin{matrix} \frac{\partial θ}{\partial t} \end{matrix}$ =∇[k(h)∇(H)]-S(4)

式中:θ 表示土壤体积含水率; t是时间; h是土壤水势; k是非饱和土壤导水率; H是总的土壤水势; S是根对水分的吸收速率。

宏观根吸水模型的分类和发展就是围绕着汇源项S (根系吸水项)展开的, 根据S的不同构建原理和方法, 宏观根吸水模型也划分为不同的类型。本研究将宏观模型主要分为两大类, 一类是由微观模型引申而来的Ⅰ 型模型, 另一类是基于土壤水势的经验性的Ⅱ 型模型。

2.2.1 Ⅰ 型模型基于Gardner建立的描述水分由土壤传输到根的微观尺度的物理方法, Cardon等^[19]提出了通用的Ⅰ 型模型, 其基本表达形式如下:

S=BKG(5)

式中:S代表根对水分的吸收速率; K是传导项; G是从土壤到根的水势梯度; B是描述水分运动的几何参数。

在很多文献中都有采用Ⅰ 型模型来描述根从土壤中吸收水分^{[20, 21]}, 事实上微观的根吸水模型也属于Ⅰ 型模型。宏观模型中应用Ⅰ 型模型的典型就是基于水势梯度的欧姆定律模型, 其表达式如下:

S(z)= $\begin{matrix} \frac{σ (z)}{r_{soil} (z) + r_{root}} \end{matrix}$ [H_soil(z)-H_root](6)

该模型是在微观的欧姆定律模型的基础上升级而得到的, 式中:S(z)代表深度z处根对水分的吸收速率; r_soil(z)和r_root分别代表该深度处土壤和根对水分传输的阻力; H_soil(z)和H_root分别是深度z处土壤的水势和根木质部的水势; σ (z)是深度z处有效的根吸水表面积, 可由根际半径和根半径计算获取。该模型的应用需要量化一系列的土壤和根的参数, 包括根长密度、根的平均半径、根的径向阻力、非饱和土壤导水率等^[22]。

欧姆定律模型的建立是基于一系列简单的恒定的不随时间变化的阻力项假设, 但是, 事实上植物的根系统极为复杂, 类似于混联的传输网络, 每一部分的阻力项都不相同。并且根的阻力也受到植物的蒸腾速率以及根木质部水势梯度影响^[23], 例如气穴现象会导致根木质部导水率的下降, 阻力增加^[18]。因而, 欧姆定律模型在确定阻力项方面存在很大的缺陷, 应用的准确性有限。

Ⅰ 型模型的水分吸收项对土壤盐分的含量不敏感, 在土壤的盐浓度增加时植物的蒸腾量并没有降低。因而在盐分胁迫下, 该模型的应用受到局限^[19]。

2.2.2 Ⅱ 型模型在根区土壤剖面内部, 根对土壤水分的吸收受到根区土壤水势的影响, 在这个原理的基础上, Feddes等^[24]在1978年提出了基于土壤水势的经验性根系吸水模型, 即Ⅱ 型模型, 其基本模型表达式如下:

S_a(z)=α [h(z)]S_p(z)(7)

式中:α [h(z)]是指无量纲的水分胁迫指数(也称土壤水势响应函数), 代表深度z处的水分胁迫指数, 和根区土壤的水势有关, 0≤ α [h(z)]≤ 1。α [h(z)]=0时表明根对水分的吸收速率为0, α [h(z)]=1时表明根对水分的吸收速率达到潜在的最大值。S_a(z)是深度z处实际的根吸水量, S_p(z)是深度z处潜在的根吸水量, 与实际微气象条件下植物的潜在蒸腾速率有关。

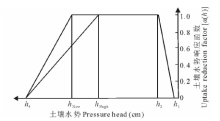
在该模型的发展过程中, 出现了多种类型的土壤水势响应函数, 包括简单的2个参数阈值的S型曲线函数以及复杂的包括5个参数的Feddes类型的函数(图1, 公式8), 应用较多的是Feddes模型^[25]。

α [h(z)]= $\begin{matrix} \{\begin{matrix} 0 & h \geq h_{1} \\ \frac{h_{1} - h}{h_{1} - h_{2}} & h_{1} > h \geq h_{2} \\ 1 & h_{2} > h \geq h_{3} \\ \frac{h - h_{4}}{h_{3} - h_{4}} & h_{3} > h \geq h_{4} \\ 0 & h \leq h_{4} \end{matrix} \end{matrix}$ (8)

图1是公式8的图形展示, 图1与公式8中的h₁表示饱和土壤中的厌氧点水势(水势一般为0), h₂是氧气胁迫的临界水势, h₃是水分胁迫的临界水势, h₄表示植物萎蔫点的水势。在区间[h₂, h₃]之间, 根对水分的吸收速率达到潜在的最大值。在区间(h₁, h₂)和(h₃, h₄)之间根对水分的吸水速率线性降低, 这种变化分别是受到氧气胁迫和水分胁迫而产生的。当h≤ h₄和h≥ h₁时根对水分的吸收速率为0。该模型的关键在于确定h₂和h₃的大小, 这两个数值随着植物的类型和土壤质地的不同将发生变化, h₂的取值一般接近于0, 而h₃的取值与植物的蒸腾速率有关, h₃_high和h₃_low分别代表植物蒸腾速率高和低时的h₃取值。

	Figure Option View Download New Window
	图1 土壤水势响应函数^[24]Fig.1 Water stress uptake reduction function of Feddes et al^[24]

Ⅱ 型模型的基本模型仅考虑了根区土壤水势对根吸收水分的影响, 但是根对水分的吸收不仅与根区的土壤水势有关, 同时也与根在土壤中的吸水分布有关。在水分不受限制的土壤剖面中, 根对水分的吸收和根在土壤中的密度分布密切相关; 而在水分缺乏的土壤剖面中, 根对土壤水分的吸收和土壤的水势呈正比。另外, 土壤水势影响函数不仅与氧气浓度、土壤水势有关, 同时也与土壤的盐分浓度有关, 这些因素都应该考虑在内。

1) 引入根系吸水分布参数的模型

考虑到在整个根区根系潜在吸水速率的非均一性分布, 在基本模型中引入根吸水分布参数项后, 就得到了升级的根吸水衰减模型, 其表达式如下:

S_a(z)=β (z)α [h(z)]T_p(9)

式中:T_p是植物潜在的蒸腾量; β (z)表示根在土壤剖面中的分布函数, 是一个相对值, 其满足

$\begin{matrix} \int_{ΩR} β (z) dR = 1 \end{matrix}$ (10)

β (z)= $\begin{matrix} \frac{R (z)}{\overset{}{\int_{ΩR}} R (z) dz} \end{matrix}$ (11)

式中:Ω R代表整个根区; R(z)代表深度z处的根长密度, 根系在土壤剖面中的密度分布函数如图2所示^{[26, 27, 28]}。

该模型同时考虑了根在土壤剖面中的吸水分布与土壤水势对根吸收水分的影响。但是, 该模型也存在着不足。首先, 模型中根吸水分布的参数大都是依据根长密度分布建立的。事实上, 研究表明控制根对水分吸收的是根的表面积而不是根长密度, 并且根吸水的主要部位仅位于根尖的一定部位^[29], 同时根有效的吸水分布项并不是常数, 它随着根的生长和衰败而不断的发生变化, 也就是说根的吸水分布项是动态的^[18]。而这种建立在静态的仅以根长密度来替代根在土壤中吸水分布的参数还需进一步的修正。其次是模型假设有效吸水根与土壤剖面中的根密度分布以及土壤的水势呈正比。这也就是说根对水分的吸收是一个被动的过程, 仅仅受到大气条件以及可利用土壤水分的分布和根的密度分布的影响。但是, 事实上瞬时的根吸水速率的空间分布和根密度的分布并不呈显著的相关关系, 这种情况在异质性的土壤结构中更加显著。同时, 对于那些具有水力再分配的植物, 应用这种模型时就忽略了根在植物水分吸收过程中的调节作用, 很可能低估了异质性土壤中植物的蒸腾^[30]。因此, 在根系吸水模型中应考虑植物根系对土壤水分再分配这一过程。

	Figure Option View Download New Window
	图2 不同的根长密度分布函数^[3]Fig.2 Various root length density distribution functions^[3]

2) 蒸腾分割模型

根系吸收水分的动力可以理解为由叶片的蒸腾失水引起的, 正是这种蒸腾散失水分的速率在很大程度上决定了根系吸收水分的速率, 蒸腾分割模型就是依据根吸收水分的因果关系建立的^[7]。植物通过根系吸收的水分90%以上被植物的蒸腾散失掉, 只有很少一部分用于植物自身的新陈代谢和生长需要, 因此可以将潜在的蒸腾量定义为整个根区深度L范围内根吸收水分的积分。

$\begin{matrix} T_{p} = \int_{0}^{L} S_{p} (z) dz \end{matrix}$ (12)

式中:T_p是植物的潜在蒸腾量; L是根区的深度; S_p(z)代表根在土壤深度z处潜在的水分吸收量。根据方程(12)可以得到蒸腾分割模型的一般表达式即:

S_p(z)=β (z)T_p(13)

该模型的建立是将潜在的蒸腾量T_p按一定的权重因子分配到不同深度的根系, 权重因子β (z)一般用根长密度分布来代替, 然后得到根在每层土壤中潜在的水分吸收量S_p(z)。

根系的吸水强度随土壤剖面的变化很大程度上与根系密度在土壤中的分布有关, 根系在土壤中的分布类型有线性的、非线性的、指数型的等。因此蒸腾分割模型也可划分为相应的线性、非线性和指数模型等。

蒸腾分割模型其实也是Ⅱ 型模型中的一种, 对于引入根系吸水分布参数的模型, 即公式S_a(z)=β (z)α [h(z)]T_p, 当α [h(z)]=1, 即植物在整个根区不受到水分胁迫时, 就得到了蒸腾分割模型。

蒸腾分割模型理论清晰, 经验性较强。但是也存在着明显的不足, 首先, 根的吸水分布参数仍是基于根长密度建立的, 其次是假设植物不受到胁迫限制, 这样就大大限制了模型的应用范围。因此, 蒸腾分割模型还有很大的发展空间, 可以将胁迫项以及根在吸水过程中的调节作用考虑在内, 建立符合实际情形的模型并扩大应用范围。

3) 带有补偿机制的根系吸水模型

一些植物能够通过其根系来调整植物的吸水方式来应对土壤水分的异质性分布, 也就是说植物在面对根区非一致的水分胁迫时, 其根系能够从胁迫低的土壤区域增加水分吸收来补偿高胁迫的土壤区域^[31], 这种根吸水的机制称之为补偿机制。补偿机制事实上就是根对土壤水分的再分配, 即根作为有效的水力传导组织通过连接不同的土壤区域来深刻影响土壤剖面中水分的分布^[32]。根对土壤水分的再分配包括水力提升、水分通过根的侧向输送和向下输送。

在灌溉或者排水产生的根区非一致的水分胁迫情形下, 补偿机制的根系吸水在其中可能起着重要的作用, 这些情况包括亏缺灌溉、部分根区干燥等^[33]。补偿机制的根吸水模型有很多, 最早提出补偿机制的根吸水模型的是Jarvis^[31]。带有补偿机制的宏观根吸水模型可以表示为:

S_a(z)=T_pα [h(z)]β (z)φ (14)

式中:φ 是补偿吸水方程。

φ = $\begin{matrix} \{\begin{matrix} \frac{1}{ω} & ω \geq ω_{c} \\ \frac{1}{ω_{c}} & ω < ω_{c} \end{matrix} \end{matrix}$ (15)

式中:ω 是加权的植物的水分胁迫指数(0< ω < 1)。

$\begin{matrix} ω = \frac{T_{a}}{T_{p}} = \int_{0}^{L} α [h (z)] β (z) dz \end{matrix}$ (16)

式中:T_a和T_p分别代表植物实际蒸腾量和潜在蒸腾量。ω _c是植物水分胁迫的临界阈值, 它的取值依赖于植物的潜在蒸腾、根的半径和根长密度分布以及土壤的水力特性。加权的水分胁迫指数ω 与土壤水势影响函数α [h(z)]的不同之处在于, α [h(z)]是描述局部的水分胁迫指数, 与根区土壤深度z处的水势和根土之间的水分传导阻力有关, 而ω 是反映植物应对干旱时整体的胁迫响应参数, 是建立在整个根区之上的^[34]。

由图3可知, 在补偿的吸水机制中, 只要加权的胁迫指数ω 大于规定的阈值ω _c(ω > ω _c), 植物的实际蒸腾就维持在潜在的水平。通过在整个根区乘以系数1/ω 来获得潜在的吸水量, 即整个根区增加吸水的效应相同。但是事实上, 增加最大的吸水效应区域发生在胁迫小、根密度大的地方, 相反则增加的吸水效应可以忽略。因此, 根区胁迫区域的根对水分的吸收从其他区域得到了充分的补偿。当根区遭受的胁迫较大(ω < ω _c)时, 补偿仅存在于部分根区, 整个根区的补偿吸收项通过乘以系数1/ω _c来获得。

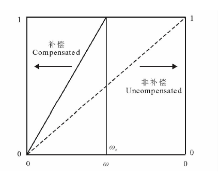	Figure Option View Download New Window
	图3 实际蒸腾和潜在蒸腾的比率与胁迫指数ω 的关系^[25] Fig.3 Ratio of the actual to potential transpiration as a function of the stress index ω ^[25]

对于具有水力再分配的植物, 在根区土壤水分呈现不一致的分布时, 补偿性的根系吸水机制在模拟土壤水分向根输送的过程中起着重要的作用, 若遗漏补偿吸收项将会导致对异质性土壤中植物蒸腾量的低估。另外, 先前的研究都认为根吸水的补偿机制是植物在遭受水分胁迫下产生的, 但是Albasha等^[8]的研究表明, 根吸水的补偿机制与植物的水分胁迫是独立的, 只要存在异质性的土壤水势分布, 即使是在相对湿润的土壤中, 植物的根系也会产生补偿作用。

现在应用的补偿机制的根吸水模型也存在着不足。首先, 胁迫阈值ω _c很难获取, 同时该模型也存在着概念上的缺陷。为了弥补补偿机制概念上的缺陷, Peters^[34]对该模型进行了修正, 使得补偿机制的根吸水模型在均质性胁迫的土壤、均质性根分布以及部分根区根的分布趋近为0时的模型模拟准确性都大大提升。

4) 引入基质通量势的根吸水模型

由于上述补偿机制的根吸水模型经验性较强, 同时对机理方面的知识描述太少, 并且涉及的参数难以获取。因而引入了基质通量势的方法建立了基于物理机制的补偿根吸水模型。这种基于物理机制方法的一个最重要的优点就是在经验模型中无量纲的胁迫参数和可测量的系统参数之间建立了明确的相关关系, 这些可获取的系统参数包括根长密度参数和根的导水参数等^[35]。

基质通量势是某一土体非饱和导水率的积分, 是线性化的描述水分径向流入到根的土壤导水特性的参数, 和土壤水分运动、根对水分的吸收以及受限制的土壤水力条件紧密相关的土壤的物理特性^[36]。

$\begin{matrix} M = \overset{h}{\int_{h_{w}}} K (h) dh \end{matrix}$ (17)

式中:h和h_w分别代表当前的土壤水势和永久萎蔫点的水势, K是土壤的导水率。选择萎蔫点的水势作为下限表明当h=h_w时, M=0。

基于基质通量势的宏观根吸水模型可以表示为:

S_a(z)=ρ (M-M₀)(18)

式中:S_a(z)是根在土壤深度z处的水分吸收量; M是该层土壤的基质通量势; ρ 是依赖于根长密度和根半径的复合参数; M₀是根表面的基质通量势(假设其在整个根区为常数)。根在每层土壤中吸收的水分与该层土壤的基质通量势和根表面的基质通量势有关^{[37, 38]}。

用基质通量势的参数将经验性根吸水补偿机制模型中的相关参数进行替换, 便得到了基于物理机制的宏观补偿机制的根吸水模型。这种替换包括, 例如:ω _c=E_p/[(∑ _iρ iΔ zi)M_max], α [h(z)]=M/M_max等^[39]。这种建立在物理机制上的补偿根吸水模型机理性更强也更加有说服力, 使得那些难以获取的参数有了计算的标准, 同时也说明了经验性的补偿吸水模型是机理性吸水模型的一种简化形式^[39]。

2.3 其他根系吸水模型

2.3.1 多维度根吸水模型的发展早期的根系吸水模型聚焦于简单的一维形式, 如Gardner的单根径向流动模型。近年来模型的发展越来越涉及复杂的根结构和相关的土壤和植物过程的二维和三维模型^{[5, 39, 40]}。一维模型代表根对土壤水分的线性吸收, 二维模型代表面状吸收, 三维模型代表根在土壤剖面中的立体吸收。三维根吸水模型是根吸水模型发展的趋势, 因为它最能反映根在土壤中吸收水分的实际情况, 同时随着计算机模拟技术和相应的生物物理技术的发展使得深入研究三维根吸水模型成为了可能。应用较广的三维模型有Hydrus-3D, R-SMWS模型等^{[5, 40]}。

2.3.2 水盐胁迫下的根吸水模型在干旱半干旱区, 植物常遭遇水分和盐分的共同胁迫, 水盐胁迫都会使根对水分的吸收减少, 并且相对于单独水、盐胁迫, 植物在水盐共胁迫下需要消耗更多能量来吸收水分^[41]。宏观根系吸水模型很少涉及水盐共同胁迫下的根系吸水机制, 这种模型在干旱半干旱区应用中必然受到一定的局限性。然而水盐胁迫下根系吸水的定量研究, 对于干旱半干旱区农作物产量的提升和水资源的管理尤为重要^[42]。

水盐共胁迫对根系吸水的影响主要体现在根系细胞的渗透势方面。水分胁迫和盐分胁迫交互作用下对根吸收水分的影响包括两个假设。第一, 水分和盐分胁迫对根吸收水分的影响效应是相加的; 第二, 这种交互作用的影响效应是相乘的^[43]。最初的水盐共胁迫模型是建立在Feddes模型之上, 将盐分胁迫对根吸水的影响引入到水势响应函数中。尽管水盐共胁迫的根吸水模型经过了很多年的发展, 但是怎样将水分胁迫效应和盐分胁迫效应进行结合仍然是该类模型发展面临的最主要挑战。

3 面临的挑战和研究展望

根系吸水模型虽然经过了几十年的发展, 分类更加健全完善, 模拟效果也越来越好。但是, 由于根生长在地下, 受到观测手段的局限性以及相关理论知识的缺乏, 已有的根系吸水模型在模拟的准确性方面还有相当程度的不足。一个准确的应用广泛的根系吸水模型应当具备两个特点:科学性和简洁性。即在机理性上模型应当考虑的更加全面深入, 而在模型的组成上应趋向于简单, 精简模型中的参数, 只考虑对模型贡献最大的相关参数, 当模型具备了这两个特性才能决定其应用的普遍性。在未来根系吸水模型的发展面临的挑战和展望包括以下几个方面。

3.1 根系吸收水分参数的准确界定

在很多根系吸水模型中都有涉及根土界面的水势、根和土壤对水分传输的阻力等参数, 这些参数的完善对建立准确的根系吸水模型十分重要。但是现在对这些参数的界定有着一定的局限性, 因为这些参数都是微观尺度上的, 准确的界定需要高精度灵敏的测量技术的发展。

3.2 夜间根系吸水的重要性

大多数的土壤-植物-大气连续体模型都假设夜间没有发生根对水分的吸收, 因为此时的蒸腾速率为0^[44]。但是很早就有研究知道景天酸(CAM)类的植物夜间的气孔是开放的。另外一些C₃和C₄类型的植物也具有夜间蒸腾, 这就要求应当深入研究夜间根对土壤水分的吸收, 进而来完善根系吸水模型的发展^[9]。

3.3 动态的根系吸水模型的建立

现有的根吸水模型都是在根的静态基础上建立的, 但是实际上根在土壤中随着时间的变化而不断的生长, 进行着老根死亡新根产生的更新。因而, 根吸水模型的建立应将动态的根生长状况考虑在内, 以达到与实际情形的符合。

3.4 宏观与微观模型相结合

宏观的根吸水模型侧重于经验性和应用性, 模型的参数也较为简化, 均是在描述土壤水分运动的理查德方程上外加一个根系吸水项来表示。但是几乎所有的吸水项的建立都是将根系统进行简化, 对根系统的详细剖析相当缺乏, 同时对于根吸水的机理方面考虑也不够充分。微观的根吸水模型是建立在单根尺度上的, 对根吸水的生理机理方面阐释得很清晰, 但是很难将这种建立在单根尺度上的模型扩展到整个根系统或者是更大的尺度上, 实际的应用性受到局限。因而, 将宏观和微观的根吸水模型进行整合建立复合的根吸水模型更能准确的描述植物根系对水分的吸收情况, 这也是根系吸水模型发展的趋势^[45]。

3.5 树木和草类根系吸水模型的建立

多数的根系吸水模型都是有关农作物的, 例如小麦(Triticum aestivum)、玉米(Zea mays)等, 而有关树木和草类的根系吸水模型在现有的文献中并不多见。由于树木根系吸水模型研究的复杂性, 使得多数研究都侧重于直径不大的小树, 但是, 树木根系吸水必定会在其生长周期的不同阶段发生变化。因而, 伴随着相关技术和理论知识的发展, 树木的根系吸水模型应当会受到关注并不断完善。草原面积约占我国土地总面积的49.04%, 同时面临着不同程度的草场退化、沙漠侵蚀、面积萎缩、草场质量下降等问题^[46]。建立树木和草类根系的吸水模型, 弄清树木和草类的需水规律在保护干旱半干旱地区植物, 维系脆弱的生态环境方面具有重要意义。

由于根系吸水模型研究的重要性和现有模型应用的局限性, 使得根系吸水模型有待于进一步发展。伴随着相应的先进观测手段和实验方法的突破, 以及有关根系吸水理论的进一步完善, 根吸水模型的构建一定会有重大的进展。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Taiz L, Zeiger E. Plant Physiology[M]. Song C P, Wang X L, trans. Fourth Edition. Beijing: Science Press, 2009. Taiz L, Zeiger E. 植物生理学[M]. 宋纯鹏, 王学路, 译. 第四版. 北京: 科学出版社, 2009. [本文引用:2]
[2]	Feddes R A, Hoff H, Bruen M, et al. Modeling root water uptake in hydrological and climate models. Bulletin of the American Meteorological Society, 2001, 82(12): 2797-2809. [本文引用:1]
[3]	Kumar R, Shankar V, Jat M K. Evaluation of root water uptake models-a review. ISH Journal of Hydraulic Engineering, 2015, 21(2): 115-124. [本文引用:2]
[4]	Jarvis N J. Simple physics-based models of compensatory plant water uptake: concepts and eco-hydrological consequences. Hydrology and Earth System Sciences, 2011, 15(11): 3431-3446. [本文引用:1]
[5]	Javaux M, Schroder T, Vand erborght J, et al. Use of a three-dimensional detailed modeling approach for predicting root water uptake. Vadose Zone Journal, 2008, 7(3): 1079-1088. [本文引用:4]
[6]	Quijano J C, Kumar P, Drewry D T, et al. Competitive and mutualistic dependencies in multi-species vegetation dynamics enabled by hydraulic redistribution. Water Resources Research, 2012, 48: 1-22. [本文引用:1]
[7]	Ji X B, Kang E S, Chen R S, et al. Research advances about water-uptake models by plant roots. Acta Botanica Boreali-Occidentalia Sinica, 2006, 26(5): 1079-1086. 吉喜斌, 康尔泗, 陈仁升, 等. 植物根系吸水模型研究进展. 西北植物学报, 2006, 26(5): 1079-1086. [本文引用:2]
[8]	Albasha R, Mailhol J C, Cheviron B. Compensatory uptake functions in empirical macroscopic root water uptake models-Experimental and numerical analysis. Agricultural Water Management, 2015, 155: 22-39. [本文引用:5]
[9]	Green S R, Kiskham M B, Clothier B E. Root uptake and transpiration: From measurements and models to sustainable irrigation. Agricultural Water Management, 2006, 86(1/2): 165-176. [本文引用:2]
[10]	Marzec M, Melzer M, Szarejko I. Root hair development in the grasses: what we already know and what we still need to know. Plant Physiology, 2015, 168(2): 407-414. [本文引用:1]
[11]	Gardner W R. Dynamic aspects of water availability to plants. Soil Science, 1960, 89(2): 63-73. [本文引用:2]
[12]	Steudle E, Peterson C A. How does water get through roots. Journal of Experimental Botany, 1998, 49: 775-788. [本文引用:1]
[13]	Yang P L, Hao Z Y. Development of plant root uptake models. Journal of China Agricultural University, 1999, 4(2): 67-73. 杨培岭, 郝仲勇. 植物根系吸水模型的发展动态. 中国农业大学学报, 1999, 4(2): 67-73. [本文引用:1]
[14]	Vand enhonert T H. Water transport in plants as a catenary process. Discussions of the Faraday Society, 1948, 3: 146-153. [本文引用:1]
[15]	Gardner W R. Dynamic aspects of soil-water availability to plants. Annual Review of Physiology, 1965, 16: 323-342. [本文引用:1]
[16]	Campbell G S. Soil Physics with BASIC: Transport Models for Soil-plant Systems[M]. Amsterdam: Elsevier, 1985. [本文引用:1]
[17]	Shao M A. A model of soil moisture extraction by plant roots. Progress in Soil Science, 1986, 3: 6-15, 28. 邵明安. 植物根系吸收土壤水分的数学模型. 土壤学进展, 1986, 3: 6-15, 28. [本文引用:1]
[18]	Hopmans J W, Bristow K L. Current capabilities and future needs of root water and nutrient uptake modeling. Advance in Agronomy, 2002, 77: 103-183. [本文引用:3]
[19]	Cardon G E, Letey J. Plant water uptake terms evaluated for soil water and solute movement models. Soil Science Society of America Journal, 1992, 56(6): 1876-1880. [本文引用:2]
[20]	Feddes R A, Bresler E, Newman S P. Field test of a modified numerical model for water uptake by root systems. Water Resources Research, 1974, 10(6): 1199-1206. [本文引用:1]
[21]	Nimah M N, Hanks R J. Model for estimating soil water, plant, and atmospheric interrelations. I. Description and sensitivity. Soil Science of America Journal, 1973, 37(4): 522-527. [本文引用:1]
[22]	Vogel T, Dohnal M, Dusek J, et al. Macroscopic modeling of plant water uptake in a forest stand involving root-mediated soil water redistribution. Vadose Zone Journal, 2013, 12(1): 1-12. [本文引用:1]
[23]	Passioura J B. Water transport in and to roots. Annual Review of Plant Physiology and Molecular Biology, 1988, 39: 245-265. [本文引用:1]
[24]	Feddes R A, Kowalik P J, Zaradny H. Simulation of Field Water Use and Crop Yield[M]. Wageningen: Centre for Agricultural Publishing and Documentation, 1978. [本文引用:1]
[25]	Šimūnek J, Hopmans J W. Modeling compensated root water and nutrient uptake. Ecological Modelling, 2009, 220(4): 505-521. [本文引用:1]
[26]	Hoogland J C, Feddes R A, Belmans C. Root water uptake model depending on soil water pressure head and maximum extraction rate. Acta Horticulturae, 1981, 119: 123-136. [本文引用:1]
[27]	Li K Y, Boisvert J B, De Jong R. An exponential root water uptake model. Canadian Journal of Soil Science, 1999, 79(2): 333-343. [本文引用:1]
[28]	Prasad R. A liner root water uptake model. Journal of Hydrology, 1988, 99(3/4): 297-306. [本文引用:1]
[29]	Varney G T, Canny M J. Rates of water uptake into the mature root system of maize plants. New Phytologist, 1993, 123(4): 775-786. [本文引用:1]
[30]	Kuhlmann A, Neuweiler I, Helmig R, et al. Influence of soil structure and root water uptake strategy on unsaturated flow in heterogeneous media. Water Resources Research, 2012, 48: 229-235. [本文引用:1]
[31]	Jarvis N J. A simple empirical model of root water uptake. Journal of Hydrology, 1989, 107(1/4): 57-72. [本文引用:2]
[32]	Nadezhdina N, David T S, David J S, et al. Trees never rest: the multiple facets of hydraulic redistribution. Ecohydrology, 2010, 3(4): 431-444. [本文引用:1]
[33]	Leib B G, Caspari H W, Redulla C A, et al. Partial root zone drying and deficit irrigation of ‘Fuji’ apples in a semi-arid climate. Irrigation Science, 2006, 24(2): 85-99. [本文引用:1]
[34]	Peters A. Modified conceptual model for compensated root water uptake-A simulation study. Journal of Hydrology, 2016, 534: 1-10. [本文引用:2]
[35]	Jarvis N. Comment on “Macroscopic root water uptake distribution using a matric flux potential approach”. Vadose Zone Journal, 2010, 9(2): 499-502. [本文引用:1]
[36]	Raats P A C. Laterally confined, steady flows of water from sources and to sinks in unsaturated soils. Soil Science Society of America Journal, 1977, 41(2): 294-304. [本文引用:1]
[37]	van Lier Q D, Metselaar K, van Dam J C. Root water extraction and limiting soil hydraulic conditions estimated by numerical simulation. Vadose Zone Journal, 2006, 5(4): 1264-1277. [本文引用:1]
[38]	van Lier Q D, van Dam J C, Metselaar K. Macroscopic root water uptake distribution using a matric flux potential approach. Vadose Zone Journal, 2008, 7(3): 1065-1078. [本文引用:1]
[39]	Vrugt J A, van Wijk M T, Hopmans J W. One-, two-, and three-dimensional root water uptake functions for transient modeling. Water Resources Research, 2001, 37(10): 2457-2470. [本文引用:3]
[40]	Heinen M. Compensation in root water uptake models combined with three-dimensional root length density distribution. Vadose Zone Journal, 2014, 13(2): DOI: DOI:10.2136/vzj2013.08.0149. [本文引用:2]
[41]	Sepaskhah A R, Yarami N. Evaluation of macroscopic water extraction model for salinity and water stress in saffron yield production. International Journal of Plant Production, 2010, 4(3): 175-186. [本文引用:1]
[42]	Li H J, Yi J, Zhang J G, et al. Modeling of soil water and salt dynamics and its effects on root water uptake in Heihe arid wetland , Gansu, China. Water, 2015, 7(5): 2382-2401. [本文引用:1]
[43]	Skaggs T H, van Genuchten M T, Shouse P J, et al . Macroscopic approaches to root water uptake as a function of water and salinity stress. Agricultural Water Management, 2006, 86(1/2): 140-149. [本文引用:1]
[44]	Coelho M B, Villalobos F J, Mateos L. Modeling root growth and the soil-plant-atmosphere continuum of cotton crops. Agricultural Water Management, 2003, 60(2): 99-118. [本文引用:1]
[45]	Schroder T, Javaux M, Vand erborght J, et al. Implementation of a microscopic soil-root hydraulic conductivity drop function in a three-dimensional soil-root architecture water transfer model. Vadose Zone Journal, 2009, 8(3): 783-792. [本文引用:1]
[46]	Zhang S Q, Yan W G. Problems of grassland ecosystems and their countermeasures in western China. Acta Prataculturae Sinica, 2006, 15(5): 11-18. 张苏琼, 阎万贵. 中国西部草原生态环境问题及其控制措施. 草业学报, 2006, 15(5): 11-18. [本文引用:1]

2009

0.0

... 水对植物的生长必不可少,植物需要通过根系不断的从土壤中吸收水分来满足叶片的蒸腾以维持植物有机体正常的生理活动^[1] ...

... 植物根系吸水主要有两种方式,即主动吸水和被动吸水^[1] ...

2001

0.0

... 根对土壤水分的吸收和输送是土壤-植物-大气连续体系统(SPAC)的重要组成部分^[2],定量研究土-根系统中水分的运动也是水文过程模拟中的主要环节^[3] ...

2015

0.0

... 在微观模型中,土壤水分的流动被描述为柱面坐标中的运动^[3],根附近区域土壤水分的运动方程可表示为: ...

2011

0.0

... 同时,植物根系对水分的吸收不仅是地表水量平衡的主要部分,而且也是控制地表、大气和植物生长之间能量交换的重要过程^[4] ...

2008

0.0

... 根对土壤水分的吸收深刻影响着有植被覆盖的上层土壤水分含量的时空分布^[5],植物根系和周围土壤之间水分传输的强度控制着植物地上部分的水分、气体和能量交换等生态生理过程^[6] ...

... 用数学模型来模拟根对土壤水分的吸收可以将问题简单化,并且应用准确的模型可以使研究不需要实地测量就能得到可靠有效的数据^[9],但是合适准确的根系吸水模型的构建是十分困难的,因为根生长在地下难以观测,进行剖面挖掘又会对根系造成破坏,同时控制根吸水生理过程的知识还不够完善^[5],所以根系吸水模型的研究还需进一步进行下去 ...

... 近年来模型的发展越来越涉及复杂的根结构和相关的土壤和植物过程的二维和三维模型^[5,39,40] ...

... 应用较广的三维模型有Hydrus-3D,R-SMWS模型等^[5,40] ...

2012

0.0

2006

0.0

. 2006, 26(5):1079-1086 DOI:doi:10.3321/j.issn:1000-4025.2006.05.033

Research advances about water-uptake models by plant roots

植物根系吸水模型研究进展

Ji X B , Kang E S , Chen R S

吉喜斌, 康尔泗, 陈仁升

植物根系吸水模型是当前生态水文和陆面过程建模领域最为活跃的研究方向,是研究流域水文、生态、环境以及水资源可持续利用等科学问题中最为关键的部分,研究植物根系吸水的物理和生理机制及其影响因素,是建立植物根系吸水模型的基础.本文通过对植物根系吸水模型研究的回顾,讨论了水分和盐分胁迫在根系吸水中的作用、根系吸水的多维模型、根系吸水在陆面过程中的作用等问题,指出植物根系吸水模型发展所面临的问题并展望了未来的发展方向.

... 鉴于植物根系在地圈-生物圈-大气圈之间相互关联的纽带作用,许多国际合作项目,诸如国际生物圈地圈计划(IGBP)、世界气候研究计划(WCRP)等都将植物根系吸水作为其项目的核心研究主题,根系吸水模型的构建也成为生态、水文、环境等科学领域研究的热点^[7] ...

... 根系吸收水分的动力可以理解为由叶片的蒸腾失水引起的,正是这种蒸腾散失水分的速率在很大程度上决定了根系吸收水分的速率,蒸腾分割模型就是依据根吸收水分的因果关系建立的^[7] ...

2015

0.0

... 但是,根吸收水分的过程很复杂,不仅受到基因控制、根的构型、根的密度分布、根对水分的阻力等内在因素的影响,同时也受到土壤水分状况、土壤对水分传输的阻力、土壤营养水平、土壤温度、土壤通气状况、植物蒸腾等外在因素的影响^[8] ...

... 根的发育时间,新根和老根的更新速率,根系在土壤区域中的空间分布,以及土壤的理化性质、气象条件等的不同都会影响根系对水分的吸收^[8,11],并导致根系吸水速率随空间和时间的变化而发生改变 ...

... 1 微观的根系吸水模型微观的根系吸水模型是描述微观土壤区域内水分向根的运动,是基于物理机制建立在单根尺度上的,研究流向和进入典型单根的径向流,侧重于描述根吸收水分的过程机理^[8] ...

... 但是此类模型建立的假设条件有许多都是与实际情形不相符的,例如认为根是无限延伸的圆柱体、吸水特性沿根长不变、具有一致的半径等,同时由于根系系统的结构很难获取,并且随时间发生变化,同时这种建立在单根尺度上的水分吸收模型很难扩展到整个根系系统^[8] ...

... 另外,先前的研究都认为根吸水的补偿机制是植物在遭受水分胁迫下产生的,但是Albasha等^[8]的研究表明,根吸水的补偿机制与植物的水分胁迫是独立的,只要存在异质性的土壤水势分布,即使是在相对湿润的土壤中,植物的根系也会产生补偿作用 ...

2006

0.0

... 另外一些C₃和C₄类型的植物也具有夜间蒸腾,这就要求应当深入研究夜间根对土壤水分的吸收,进而来完善根系吸水模型的发展^[9] ...

2015

0.0

... 1 根系吸收水分的机理根系吸收水分的机理十分复杂,植物通过根系从土壤中吸收水分,但根的不同部位对水分的吸收速率并不是一致的,实际上根主要通过根尖的根毛区来吸收水分^[10] ...

1960

0.0

... Gardner^[11,15]在1960年建立了单根尺度上的根系吸水的数学模型,原理就是用根表面以及距根木质部一定距离的合适的边界条件在方程(1)的基础上来建立根系吸水的微观模型 ...

1998

0.0

... 径向途径即水分由土壤跨过根组织(表皮、皮层、内皮层、中柱)到达根木质部,包含了质外体运输、共质体运输和跨膜运输3个部分,轴向途径是水分沿着根木质部向上输送的过程^[12] ...

1999

0.0

. 1999, 4(2):67-73 DOI:doi:10.3321/j.issn:1007-4333.1999.02.016

Development of plant root uptake models

植物根系吸水模型的发展动态

Yang P L , Hao Z Y

杨培岭, 郝仲勇

Most kinds of plant root uptake models from the first one presented by Gardner in1960 to the latters are reviewed and classified. The characters and applicabilities arediscussed for references to the research on the theory and practice of modern water savingirrigation.

综述了自1960年Gardner第1个单根吸水模型建立以来的植物根系吸水模型，对模型加以分类，并对其优缺点和适用性进行了阐述，可供现代节水灌溉的理论和应用研究参考。

... 2 根系吸水模型根据不同的划分标准,根系吸水模型可以划分为不同的类型^[13],依据研究尺度的不同,将根系吸水模型主要划分为微观和宏观两个方面,植物根系吸水模型的发展与分类见表1 ...

1948

0.0

... 微观模型是以Vandenhonert^[14]1948年提出的悬链线假说为基础的 ...

1965

0.0

1985

0.0

... 因此,可以用模拟电流传输的欧姆定律来描述水分在这个连续体内的运动,即SPAC系统中每个模块的水流通量由该模块的水势梯度和水分阻力所决定^[16] ...

1986

0.0

. 1986, 3:6-15, 28

A model of soil moisture extraction by plant roots

植物根系吸收土壤水分的数学模型

Shao M A

邵明安

正当代研究田间土壤水分循环是以土壤—植物—大气连续统一体,(Soil—Plant—Atmosphere Continuum,简称SPAC)为基础的。土壤—植物系统是SPAC的一个重要的子系统,该系统中的水分运移、能量转换等问题,已受到许多国家中科研人员的重视,尤其是美国,在这方面的研究比较广泛和深入。这一问题已成为土壤物理、植物生理等学科的重要课题之一。晚近,由于数学、物理学、生物学向这一领域渗透,使这一领域的研究更加深化了。尤其是电子计算机的应用,对该项研究起了促进作用。

... 微观尺度的定量半定量研究能够对宏观尺度的根吸水模式存在的潜在误差进行校正和分析^[17] ...

2002

0.0

... 在实际应用中宏观模型比微观模型有着更多的优势,宏观模型不需要弄清根吸水的全部过程机理,这样就不必去研究那些难以界定的土壤和根的参数^[18] ...

... 并且根的阻力也受到植物的蒸腾速率以及根木质部水势梯度影响^[23],例如气穴现象会导致根木质部导水率的下降,阻力增加^[18] ...

... 事实上,研究表明控制根对水分吸收的是根的表面积而不是根长密度,并且根吸水的主要部位仅位于根尖的一定部位^[29],同时根有效的吸水分布项并不是常数,它随着根的生长和衰败而不断的发生变化,也就是说根的吸水分布项是动态的^[18] ...

1992

0.0

... 型模型基于Gardner建立的描述水分由土壤传输到根的微观尺度的物理方法,Cardon等^[19]提出了通用的#cod#x02160 ...

... 因而在盐分胁迫下,该模型的应用受到局限^[19] ...

1974

0.0

... 型模型来描述根从土壤中吸收水分^[20,21],事实上微观的根吸水模型也属于#cod#x02160 ...

1973

0.0

... 型模型来描述根从土壤中吸收水分^[20,21],事实上微观的根吸水模型也属于#cod#x02160 ...

2013

0.0

... 该模型的应用需要量化一系列的土壤和根的参数,包括根长密度、根的平均半径、根的径向阻力、非饱和土壤导水率等^[22] ...

1988

0.0

... 并且根的阻力也受到植物的蒸腾速率以及根木质部水势梯度影响^[23],例如气穴现象会导致根木质部导水率的下降,阻力增加^[18] ...

1978

0.0

... 型模型在根区土壤剖面内部,根对土壤水分的吸收受到根区土壤水势的影响,在这个原理的基础上,Feddes等^[24]在1978年提出了基于土壤水势的经验性根系吸水模型,即#cod#x02161 ...

2009

0.0

... 在该模型的发展过程中,出现了多种类型的土壤水势响应函数,包括简单的2个参数阈值的S型曲线函数以及复杂的包括5个参数的Feddes类型的函数(图1,公式8),应用较多的是Feddes模型^[25] ...

1981

0.0

... R(z)代表深度z处的根长密度,根系在土壤剖面中的密度分布函数如图2所示^[26,27,28] ...

1999

0.0

... R(z)代表深度z处的根长密度,根系在土壤剖面中的密度分布函数如图2所示^[26,27,28] ...

1988

0.0

... R(z)代表深度z处的根长密度,根系在土壤剖面中的密度分布函数如图2所示^[26,27,28] ...

1993

0.0

2012

0.0

... 同时,对于那些具有水力再分配的植物,应用这种模型时就忽略了根在植物水分吸收过程中的调节作用,很可能低估了异质性土壤中植物的蒸腾^[30] ...

1989

0.0

... 一些植物能够通过其根系来调整植物的吸水方式来应对土壤水分的异质性分布,也就是说植物在面对根区非一致的水分胁迫时,其根系能够从胁迫低的土壤区域增加水分吸收来补偿高胁迫的土壤区域^[31],这种根吸水的机制称之为补偿机制 ...

... 补偿机制的根吸水模型有很多,最早提出补偿机制的根吸水模型的是Jarvis^[31] ...

2010

0.0

... 补偿机制事实上就是根对土壤水分的再分配,即根作为有效的水力传导组织通过连接不同的土壤区域来深刻影响土壤剖面中水分的分布^[32] ...

2006

0.0

... 在灌溉或者排水产生的根区非一致的水分胁迫情形下,补偿机制的根系吸水在其中可能起着重要的作用,这些情况包括亏缺灌溉、部分根区干燥等^[33] ...

2016

0.0

... 是反映植物应对干旱时整体的胁迫响应参数,是建立在整个根区之上的^[34] ...

... 为了弥补补偿机制概念上的缺陷,Peters^[34]对该模型进行了修正,使得补偿机制的根吸水模型在均质性胁迫的土壤、均质性根分布以及部分根区根的分布趋近为0时的模型模拟准确性都大大提升 ...

2010

0.0

... 这种基于物理机制方法的一个最重要的优点就是在经验模型中无量纲的胁迫参数和可测量的系统参数之间建立了明确的相关关系,这些可获取的系统参数包括根长密度参数和根的导水参数等^[35] ...

1977

0.0

... 基质通量势是某一土体非饱和导水率的积分,是线性化的描述水分径向流入到根的土壤导水特性的参数,和土壤水分运动、根对水分的吸收以及受限制的土壤水力条件紧密相关的土壤的物理特性^[36] ...

2006

0.0

... 根在每层土壤中吸收的水分与该层土壤的基质通量势和根表面的基质通量势有关^[37,38] ...

2008

0.0

... 根在每层土壤中吸收的水分与该层土壤的基质通量势和根表面的基质通量势有关^[37,38] ...

2001

0.0

... [h(z)]=M/M_max等^[39] ...

... 这种建立在物理机制上的补偿根吸水模型机理性更强也更加有说服力,使得那些难以获取的参数有了计算的标准,同时也说明了经验性的补偿吸水模型是机理性吸水模型的一种简化形式^[39] ...

... 近年来模型的发展越来越涉及复杂的根结构和相关的土壤和植物过程的二维和三维模型^[5,39,40] ...

2014

0.0

... 近年来模型的发展越来越涉及复杂的根结构和相关的土壤和植物过程的二维和三维模型^[5,39,40] ...

... 应用较广的三维模型有Hydrus-3D,R-SMWS模型等^[5,40] ...

2010

0.0

... 2 水盐胁迫下的根吸水模型在干旱半干旱区,植物常遭遇水分和盐分的共同胁迫,水盐胁迫都会使根对水分的吸收减少,并且相对于单独水、盐胁迫,植物在水盐共胁迫下需要消耗更多能量来吸收水分^[41] ...

2015

0.0

... 然而水盐胁迫下根系吸水的定量研究,对于干旱半干旱区农作物产量的提升和水资源的管理尤为重要^[42] ...

2006

0.0

... 第二,这种交互作用的影响效应是相乘的^[43] ...

2003

0.0

... 2 夜间根系吸水的重要性大多数的土壤-植物-大气连续体模型都假设夜间没有发生根对水分的吸收,因为此时的蒸腾速率为0^[44] ...

2009

0.0

... 因而,将宏观和微观的根吸水模型进行整合建立复合的根吸水模型更能准确的描述植物根系对水分的吸收情况,这也是根系吸水模型发展的趋势^[45] ...

2006

0.0

. 2006, 15(5):11-18 DOI:doi:10.3321/j.issn:1004-5759.2006.05.002

Problems of grassland ecosystems and their countermeasures in western China

中国西部草原生态环境问题及其控制措施

Zhang S Q , Yan W G

张苏琼, 阎万贵

草原是西部地区最脆弱的生态系统.草原生态环境建设是西部生态环境建设的主体和关键.本研究系统分析了西部地区草原的地位和作用,指出了草原生态环境状况、所面临的问题及其引发机理,查明了西部草原生态环境恶化的原因,确立了实施可持续发展模式,建立草地农业生态系统,是解决西部地区生态恶化、经济落后和社会不稳定的有效途径.总体建设上突出植被恢复和水土保持、遏制土地荒漠化;区域建设上突出水源涵养区、风沙区、水土流失区和自然保护区;产业发展上突出区域特色产业和绿色产业;项目选择上突出综合效益;技术选择上突出高新技术.并提出了西部草原生态保护、生态建设与可持续发展的对策措施.

... 04%,同时面临着不同程度的草场退化、沙漠侵蚀、面积萎缩、草场质量下降等问题^[46] ...